Traces of nilpotent matrices

Posted on 18 November 2022 by Remy

I needed the following well-known result in the course I’m teaching:

Lemma. Let $k$ be a field and $M \in M_n(k)$ a nilpotent matrix. Then $\operatorname{tr} M = 0$ .

The classical proof uses the flag of subspaces

$0 \subseteq \ker M \subseteq \ker M^2 \subseteq \ldots \subseteq \ker M^n = k^n$

to produce a basis for which $M$ is upper triangular. Here is a slick basis-independent commutative algebra proof that shows something better:

Lemma. Let $R$ be a commutative ring with nilradical $\mathfrak r$ , and let $M \in M_n(k)$ be a nilpotent matrix. Then the characteristic polynomial $p_M(t) = \det(tI-M)$ satisfies

$p_M(t) \in t^n + \mathfrak r[t]_{< n}.$

Here we write $I[t]_{<n} \subseteq R$ for the polynomials in $R$ of degree smaller than $n$ whose coefficients lie in a given ideal $I \subseteq R$ .

Note that the formulation should ring a bell: in the previous post we saw that $R[t]^\times = R^\times + t\mathfrak r[t]$ . When $R$ is a domain, this reduces to $R[t]^\times = R^\times$ , and the lemma just says that $p_M(t) = t^n$ .

This suggests that we shouldn’t work with $\det(tI-M)$ but with its anadrome (or reciprocal) $t^n\det(t^{-1}I-M) = \det(I-tM)$ .

Proof of Lemma. We have to show that $\det(I-tM) \in 1 + t\mathfrak r[t]$ . Since $M$ is nilpotent, there exists $r \in \mathbf N$ with $M^{r+1} = 0$ , so $(I-tM)(I+tM+\ldots+t^rM^r) = I$ . Thus $\det(I-tM) \in R[t]^\times = R^\times + t\mathfrak r[t]$ . Evaluating at $t=0$ shows that the constant coefficient is 1. $\qedsymbol$

Invertible polynomials

Posted on 11 November 2022 by Remy

Here is a classic little lemma on polynomials:

Lemma. Let $R$ be a commutative ring with nilradical $\mathfrak r$ . Then $R[t]^\times = R^\times + t\mathfrak r[t]$ .

That is, a polynomial $a_nt^n + \ldots + a_1t + a_0 \in R[t]$ is invertible if and only if $a_0$ is invertible and $a_1,\ldots,a_n$ are nilpotent. This is the formulation you find in Atiyah–MacDonald, exercise 1.2(i). Note that when $R$ is a domain (or more generally a reduced ring), this just says that $R[t]^\times = R^\times$ (via the constant polynomials).

Proof. First suppose $f = \sum_{i=0}^n a_nt^n$ with $a_0 \in R^\times$ and $a_1,\ldots,a_n \in \mathfrak r$ . Multiplying by $a_0^{-1}$ we may assume $a_0 = 1$ ; this does not change the nilpotence assumption on $a_1,\ldots,a_n$ . Then $g := 1-f = -a_1t-\ldots - a_nt^n$ is nilpotent since it is a sum of nilpotent elements $-a_it^i$ in the commutative ring $R[t]$ . Thus we get $g^{r+1} = 0$ for some $r \in \mathbf N$ , and

$(1-g)(1+g+\ldots+g^r) = 1$

shows that $f \in R[t]^\times$ . Conversely, let $f \in R[t]^\times$ , and suppose $fg = 1$ for some polynomial $g = b_mt^m + \ldots + b_1t+b_0 \in R[t]$ . Without loss of generality we may assume $a_n \neq 0 \neq b_m$ . If $R$ is a domain, then the leading term of $fg$ is $a_nb_mt^{m+n} \neq 0$ , so we must have $n=m=0$ and $f$ and $g$ are constant. In the general case, we conclude that $\phi(f) \in S^\times \subseteq S[t]$ for any ring homomorphism $\phi \colon R \to S$ to a domain $S$ . In particular, taking $S = R/\mathfrak p$ for any prime ideal $\mathfrak p \subseteq R$ shows $a_1,\ldots,a_n \in \mathfrak p$ and $a_0 \not\in\mathfrak p$ . Taking the intersection over all prime ideals gives

$\qedsymbol$ $\begin{align*}a_1,\ldots,a_n &\in \bigcap_{\mathfrak p \text{ prime}} \mathfrak p = \mathfrak r,\\ a_0 &\in \bigcap_{\mathfrak p \text{ prime}} (R \setminus \mathfrak p) = R^\times. \end{align*}$

The 14 closure operations

Posted on 6 November 2022 by Remy

I’ve been getting complaints that my lemmas have not been so lovely (or little) lately, so let’s do something a bit more down to earth. This is a story I learned from the book Counterexamples in topology by Steen and Seebach [SS].

A topological space $X$ comes equipped with various operations on its power set $\mathcal P(X)$ . For instance, there are the maps $S \mapsto S^\circ$ (interior), $S \mapsto \bar S$ (closure), and $S \mapsto S^{\text{c}}$ (complement). These interact with each other in nontrivial ways; for instance $(\bar S)^{\text{c}} = (S^{\text{c}})^\circ$ .

Consider the monoid $M$ generated by the symbols $a$ (interior), $b$ (closure), and $c$ (complement), where two words in $a$ , $b$ , and $c$ are identified if they induce the same action on subsets of an arbitrary topological space $X$ .

Lemma. The monoid $M$ has 14 elements, and is the monoid given by generators and relations

$M = \left\langle a,b,c\ \left|\ \begin{array}{cc} a^2=a, & (ab)^2=ab, \\ c^2=1, & cac=b.\end{array}\right.\right\rangle.$

Proof. The relations $a^2 = a$ , $c^2=1$ , and $cac=b$ are clear, and conjugating the first by $c$ shows that $b^2=b$ is already implied by these. Note also that $a$ and $b$ are monotone, and $a(T) \subseteq T \subseteq b(T)$ for all $T \subseteq X$ . A straightforward induction shows that if $v$ and $w$ are words in $a$ and $b$ , then $vaw(S) \subseteq vw(S) \subseteq vbw(S)$ . We conclude that

$abab(S) \subseteq abb(S) = ab(S) = aab(S) \subseteq abab(S),$

so $(ab)^2=ab$ (this is the well-known fact that $ab(S)$ is a regular open set). Conjugating by $c$ also gives the relation $(ba)^2 = ba$ (saying that $ba(S)$ is a regular closed set).

Thus, in any reduced word in $M$ , no two consecutive letters agree because of the relations $a^2=a$ , $b^2=b$ , and $c^2=1$ . Moreover, we may assume all occurrences of $c$ are at the start of the word, using $ac=cb$ and $bc=ca$ . In particular, there is at most one $c$ in the word, and removing that if necessary gives a word containing only $a$ and $b$ . But reduced words in $a$ and $b$ have length at most 3, as the letters have to alternate and no string $abab$ or $baba$ can occur. We conclude that $M$ is covered by the 14 elements

$\begin{array}{ccccccc}1, & a, & b, & ab, & ba, & aba, & bab,\\c, & ca, & cb, & cab, & cba, & caba, & cbab. \end{array}$

To show that all 14 differ, one has to construct, for any $i\neq j$ in the list above, a set $S_{i,j} \subseteq X_{i,j}$ in some topological space $X_{i,j}$ such that $i(S_{i,j}) \neq j(S_{i,j})$ . In fact we will construct a single set $S \subseteq X$ in some topological space $X$ where all 14 sets $i(S)$ differ.

Call the sets $i(S)$ for $i \in \langle a,b\rangle$ the noncomplementary sets obtained from $S$ , and their complements the complementary sets. By the arguments above, the noncomplementary sets always satisfy the following inclusions:
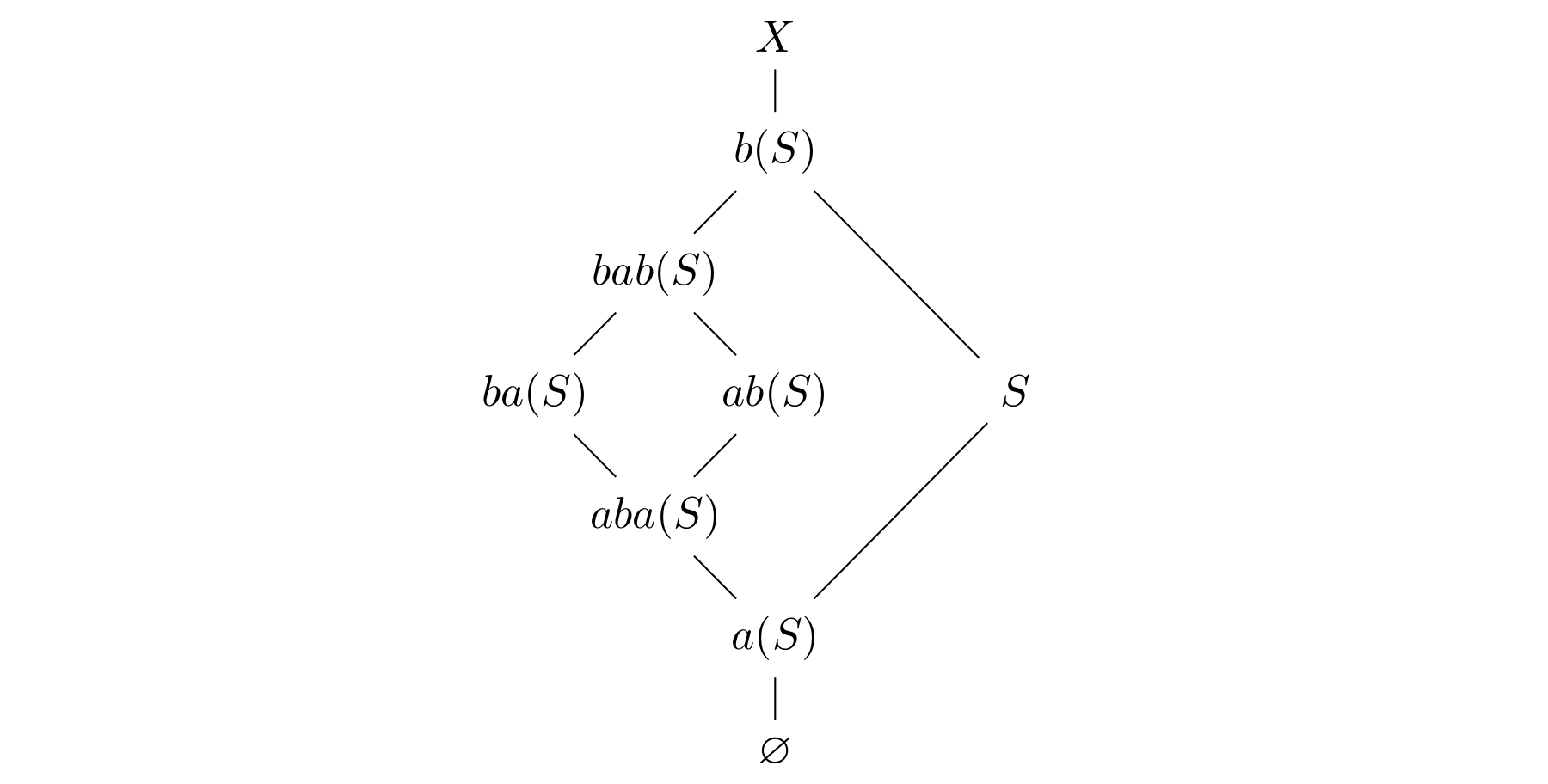It suffices to show that the noncomplementary sets are pairwise distinct: this forces $a(S) \neq \varnothing$ (otherwise $a(S) = ba(S)$ ), so each noncomplementary set contains $a(S)$ and therefore cannot agree with a complementary set.

For our counterexample, consider the 5 element poset $P$ given by

$\begin{array}{ccccc}p\!\!\! & & & & \!\!\!q \\ \uparrow\!\!\! & & & & \!\!\!\uparrow \\ r\!\!\! & & & & \!\!\!s \\ & \!\!\!\nwarrow\!\!\! & & \!\!\!\nearrow\!\!\! & \\ & & \!\!\!t,\!\!\!\!\! & & \end{array}$

and let $X$ be the disjoint union of $P^{\operatorname{Alex}}$ (the Alexandroff topology on $P$ , see the previous post) with a two-point indiscrete space $\{u,v\}$ . Recall that the open sets in $P^{\operatorname{Alex}}$ are the upwards closed ones and the closed sets the downward closed ones. Let $S = \{p,s,u\}$ . Then the diagram of inclusions becomes 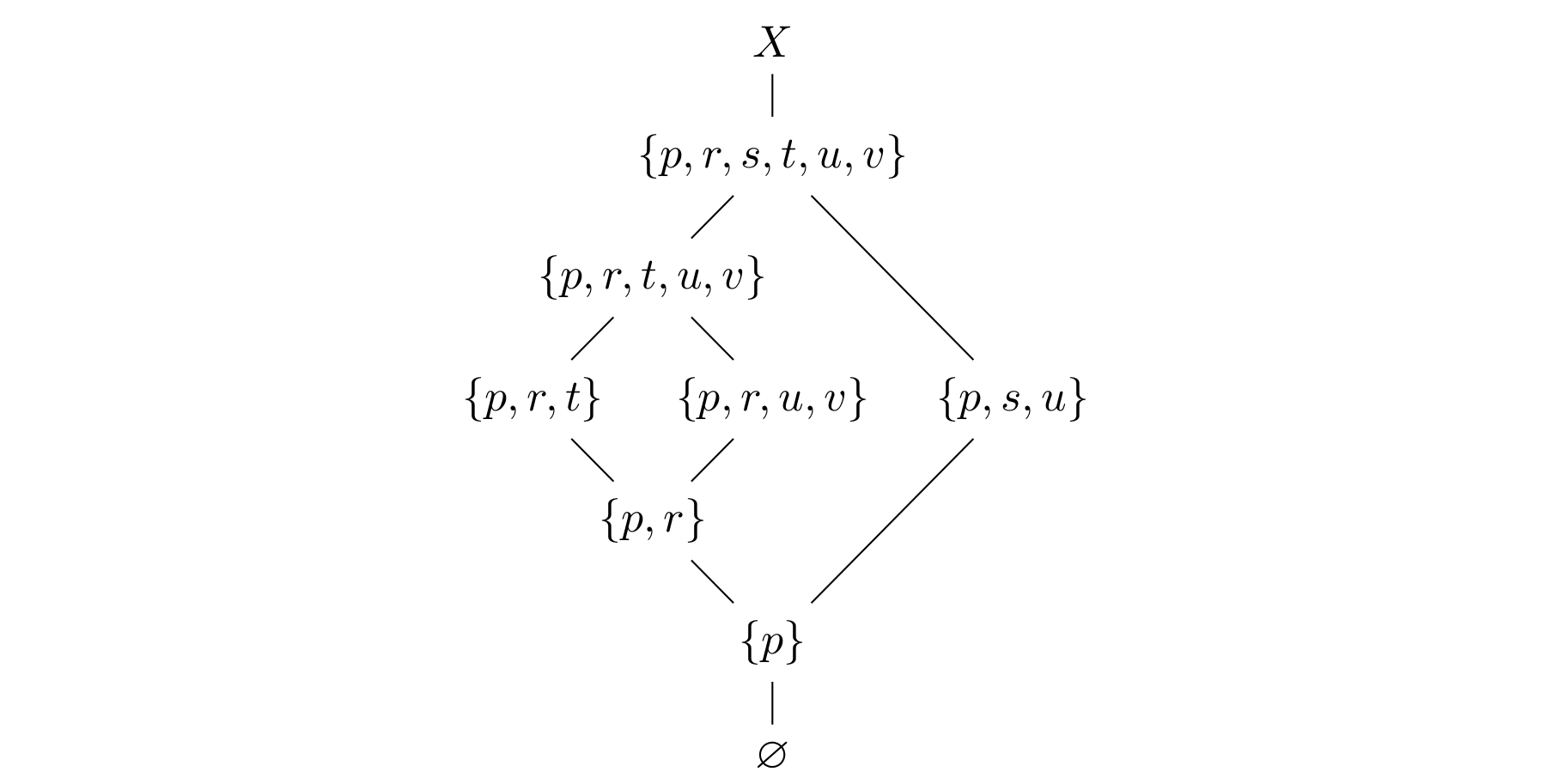We see that all 7 noncomplementary sets defined by $S$ are pairwise distinct. $\qedsymbol$

Remark. Steen and Seebach [SS, Example 32(9)] give a different example where all 14 differ, namely a suitable subset $S \subseteq \mathbf R$ . That is probably a more familiar type of example than the one I gave above.

On the other hand, my example is minimal: the diagram of inclusions above shows that for all inclusions to be strict, the space $X$ needs at least 6 points. We claim that 6 is not possible either:

Lemma. Let $X$ be a finite $T_0$ topological space, and $S \subseteq X$ any subset. Then $aba(S) = ab(S)$ and $bab(S) = ba(S)$ .

But in a 6-element counterexample $X$ , the diagram of inclusions shows that any point occurs as the difference $i(S) \setminus j(S)$ for some $i,j \in \langle a,b\rangle\setminus 1$ . Since each of $i(S)$ and $j(S)$ is either open or closed, we see that the naive constructible topology on $X$ is discrete, so $X$ is $T_0$ by the remark from the previous post. So our lemma shows that $X$ cannot be a counterexample.

Proof of Lemma. We will show that $ab(S) \subseteq aba(S)$ ; the reverse implication was already shown, and the result for $bab(S)$ follows by replacing $S$ with its complement.

In the previous post, we saw that $X$ is the Alexandroff topology on some finite poset $(X,\leq)$ . If $T \subseteq X$ is any nonempty subset, it contains a maximal element $t$ , and since $X$ is a poset this means $u \geq t \Rightarrow u=t$ for all $u \in T$ . (In a preorder, you would only get $u \geq t \Rightarrow u \leq t$ .)

The closure of a subset $T \subseteq X$ is the lower set $\bigcup_{t \in T} X_{\leq t}$ , and the interior is the upper set $\{t \in T\ |\ X_{\geq t} \subseteq T\}$ . So we need to show that if $x \in ab(S)$ and $y \geq x$ , then $y \in ba(S)$ .

By definition of $ab(S)$ , we get $y \in b(S)$ , i.e. there exists $z \in S$ with $z \geq y$ . Choose a maximal $z$ with this property; then we claim that $z$ is a maximal element in $X$ . Indeed, if $u \geq z$ , then $u \geq x$ so $u \in b(S)$ , meaning that there exists $v \in S$ with $v \geq u$ . Then $v \geq z \geq y$ and $v \in S$ , which by definition of $z$ means $v=z$ . Thus $z$ is maximal in $X$ , hence $z \in a(S)$ since $z \in S$ and $X_{\geq z} = \{z\}$ . From $z \geq y$ we conclude that $y \in ba(S)$ , finishing the proof. $\qedsymbol$

The lemma fails for non- $T_0$ spaces, as we saw in the example above. More succinctly, if $X = \{x,y\}$ is indiscrete and $S = \{x\}$ , then $aba(S) = \varnothing$ and $ab(S) = X$ . The problem is that $x$ is maximal, but $X_{\geq x} \supsetneq \{x\}$ and $x \not\in a(S)$ .