I’ve been getting complaints that my lemmas have not been so lovely (or little) lately, so let’s do something a bit more down to earth. This is a story I learned from the book Counterexamples in topology by Steen and Seebach [SS].
A topological space comes equipped with various operations on its power set
. For instance, there are the maps
(interior),
(closure), and
(complement). These interact with each other in nontrivial ways; for instance
.
Consider the monoid generated by the symbols
(interior),
(closure), and
(complement), where two words in
,
, and
are identified if they induce the same action on subsets of an arbitrary topological space
.
Lemma. The monoid has 14 elements, and is the monoid given by generators and relations
Proof. The relations ,
, and
are clear, and conjugating the first by
shows that
is already implied by these. Note also that
and
are monotone, and
for all
. A straightforward induction shows that if
and
are words in
and
, then
. We conclude that
so (this is the well-known fact that
is a regular open set). Conjugating by
also gives the relation
(saying that
is a regular closed set).
Thus, in any reduced word in , no two consecutive letters agree because of the relations
,
, and
. Moreover, we may assume all occurrences of
are at the start of the word, using
and
. In particular, there is at most one
in the word, and removing that if necessary gives a word containing only
and
. But reduced words in
and
have length at most 3, as the letters have to alternate and no string
or
can occur. We conclude that
is covered by the 14 elements
To show that all 14 differ, one has to construct, for any in the list above, a set
in some topological space
such that
. In fact we will construct a single set
in some topological space
where all 14 sets
differ.
Call the sets for
the noncomplementary sets obtained from
, and their complements the complementary sets. By the arguments above, the noncomplementary sets always satisfy the following inclusions:
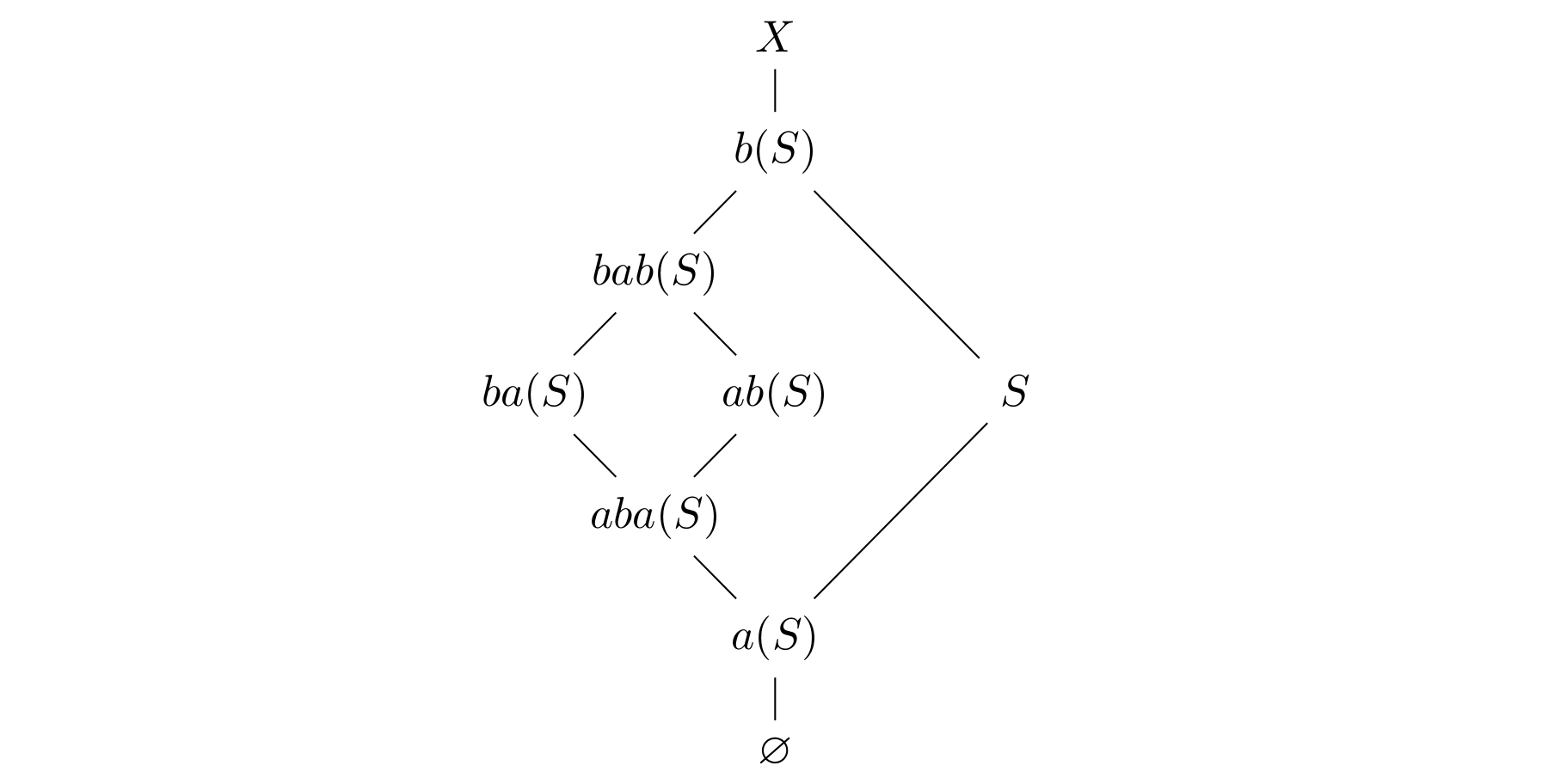 It suffices to show that the noncomplementary sets are pairwise distinct: this forces
It suffices to show that the noncomplementary sets are pairwise distinct: this forces (otherwise
), so each noncomplementary set contains
and therefore cannot agree with a complementary set.
For our counterexample, consider the 5 element poset given by
and let be the disjoint union of
(the Alexandroff topology on
, see the previous post) with a two-point indiscrete space
. Recall that the open sets in
are the upwards closed ones and the closed sets the downward closed ones. Let
. Then the diagram of inclusions becomes
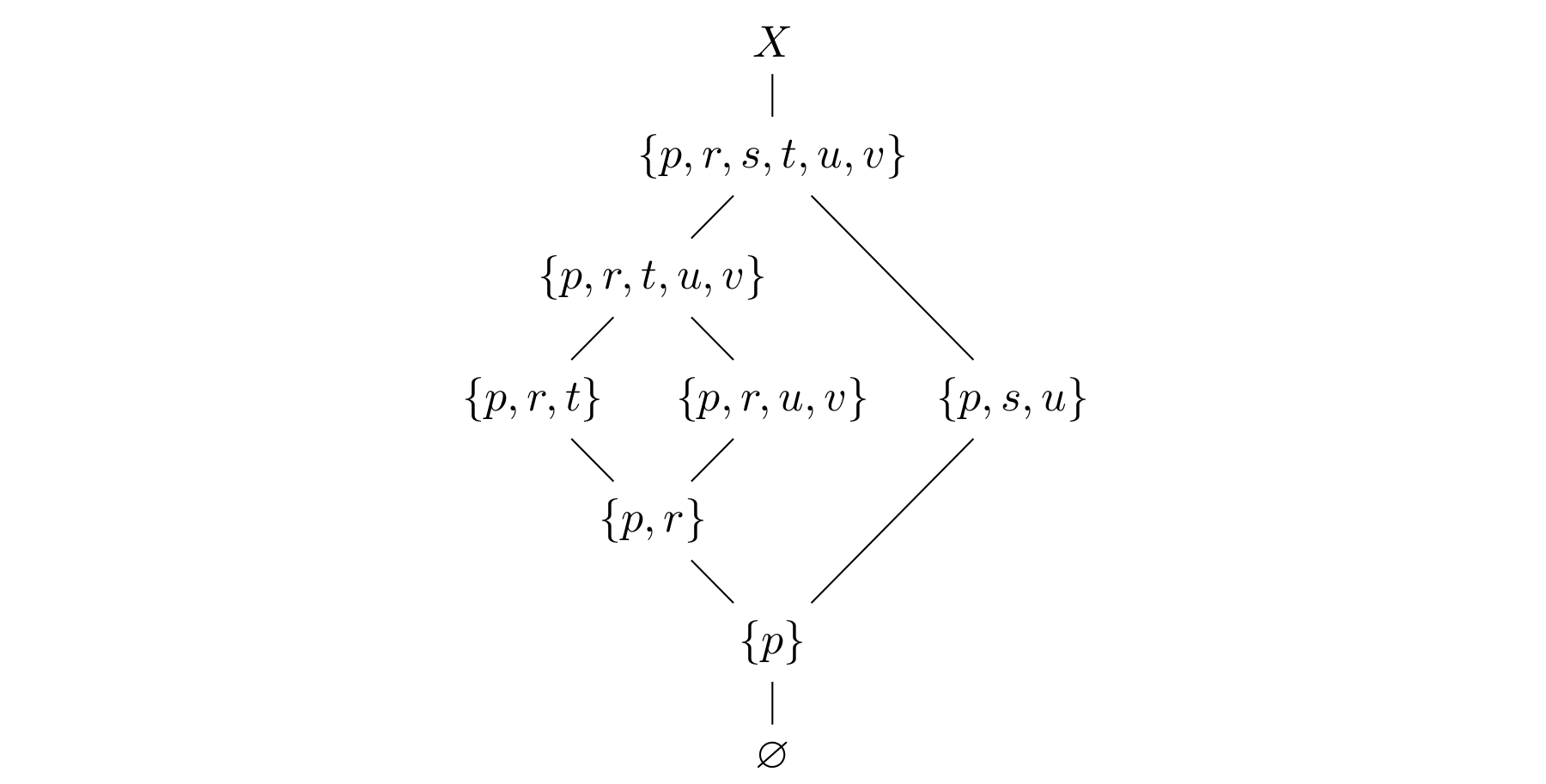 We see that all 7 noncomplementary sets defined by
We see that all 7 noncomplementary sets defined by are pairwise distinct.
Remark. Steen and Seebach [SS, Example 32(9)] give a different example where all 14 differ, namely a suitable subset . That is probably a more familiar type of example than the one I gave above.
On the other hand, my example is minimal: the diagram of inclusions above shows that for all inclusions to be strict, the space needs at least 6 points. We claim that 6 is not possible either:
Lemma. Let be a finite
topological space, and
any subset. Then
and
.
But in a 6-element counterexample , the diagram of inclusions shows that any point occurs as the difference
for some
. Since each of
and
is either open or closed, we see that the naive constructible topology on
is discrete, so
is
by the remark from the previous post. So our lemma shows that
cannot be a counterexample.
Proof of Lemma. We will show that ; the reverse implication was already shown, and the result for
follows by replacing
with its complement.
In the previous post, we saw that is the Alexandroff topology on some finite poset
. If
is any nonempty subset, it contains a maximal element
, and since
is a poset this means
for all
. (In a preorder, you would only get
.)
The closure of a subset is the lower set
, and the interior is the upper set
. So we need to show that if
and
, then
.
By definition of , we get
, i.e. there exists
with
. Choose a maximal
with this property; then we claim that
is a maximal element in
. Indeed, if
, then
so
, meaning that there exists
with
. Then
and
, which by definition of
means
. Thus
is maximal in
, hence
since
and
. From
we conclude that
, finishing the proof.
The lemma fails for non- spaces, as we saw in the example above. More succinctly, if
is indiscrete and
, then
and
. The problem is that
is maximal, but
and
.
References.
[SS] L.A. Steen, J.A. Seebach, Counterexamples in Topology. Reprint of the second (1978) edition. Dover Publications, Inc., Mineola, NY, 1995.
